

Kst provides lots of algorithms to perform data fitting. All fitting plugins output a vector of best fitted parameters, covariances, and Chi^2/Nu. These values can be seen by selecting the ->
Note: The weight is not the same as the error. It is given as 1/yError^2.
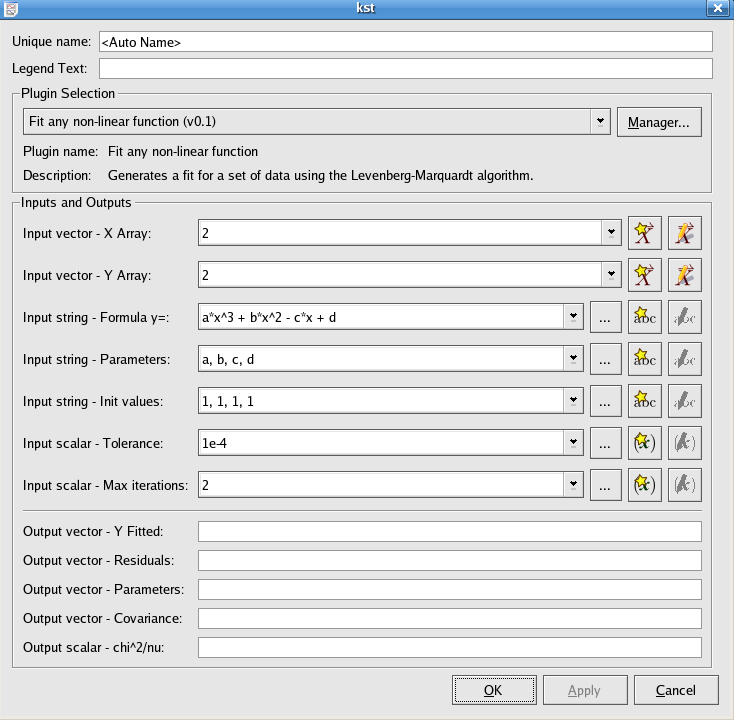
This plugin is used to fit a set of data using the Levenberg-Marquardt algorithm.
The x array of the input data set
The y array of the input data set
The formula of the curve used to fit the data set
The default string is a*x^3 + b*x^2 - c*x +d
Use a string to specify the parameter representation letters in the fitting formula. The plugin will later output the fitted values for these parameters.
The default string is a, b, c, d corresponding to the default formula string.
Use a string to specify the initial guess
The default string is 1, 1, 1, 1
Tolerance is a number to indicate the precision of fitting; if the precision reaches the tolerance value, the curve fitting will stop.
The default tolerance is 1e-4.
Specify the maximum number of iterations to indicate when the curve fitting should stop.
The default max iterations is 2.
The Y values of the fitted curve
The array of residuals
The best fitted values of the model parameters specified in the inputs.
The covariance matrix of the model parameters, returned row after row in the vector.
The sum of squares of residuals, divided by the degrees of freedom
The Fit exponential weighted plugin performs a weighted non-linear least-squares fit to an exponential model
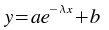
An initial estimate of
a=1.0,
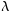
=0, and
b=0 is used. The plugin subsequently iterates to the solution
until a precision of 1.0e-4 is reached or 500 iterations have been performed.
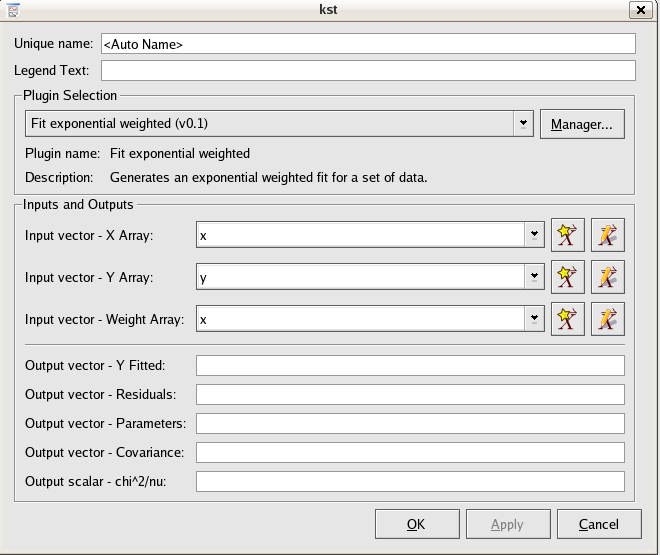
The array of x values for the data points to be fitted.
The array of y values for the data points to be fitted.
The array of weights to use for the fit.
The array of fitted y values.
The array of residuals.
The best fit parameters a,
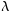 , and
, and
b.
The covariance matrix of the model parameters, returned row after row in the vector.
The weighted sum of squares of the residuals, divided by the degrees of freedom.
The Fit exponential plugin is identical in function to the
Fit exponential weighted
plugin with the exception that the weight value wi
is equal to 1 for all index values i. As a result, the
Weights (vector) input does not exist.
The Fit Gaussian weighted plugin performs a weighted non-linear least-squares fit to a Gaussian model:
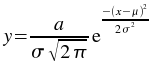
An initial estimate of
a=(maximum of the y values),
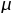
=(mean of the x values), and
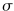
=(the midpoint of the x values)
is used. The plugin subsequently iterates to the solution
until a precision of 1.0e-4 is reached or 500 iterations have been performed.
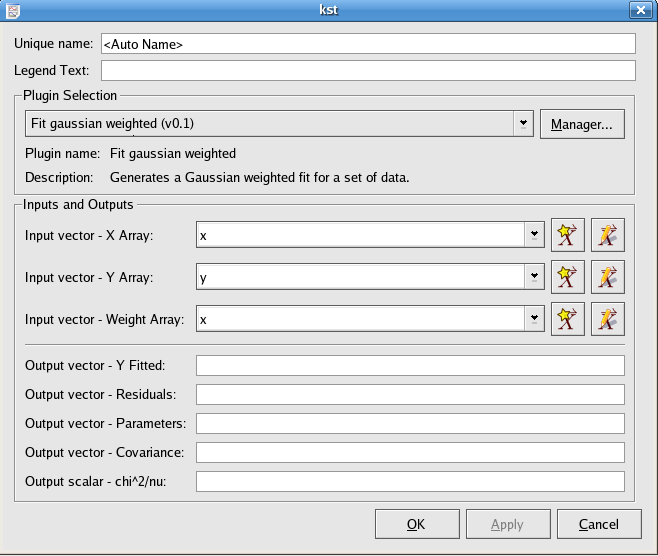
The array of x values for the data points to be fitted.
The array of y values for the data points to be fitted.
The array of weights to use for the fit.
The array of fitted y values.
The array of residuals.
The best fit parameters
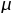 ,
,
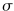 , and
, and
a.
The covariance matrix of the model parameters, returned row after row in the vector.
The weighted sum of squares of the residuals, divided by the degrees of freedom.
The Fit Gaussian plugin is identical in function to the
Fit Gaussian weighted
plugin with the exception that the weight value wi
is equal to 1 for all index values i. As a result, the
Weights (vector) input does not exist.
The gradient weighted plugin performs a weighted least-squares fit to a straight line model without a constant term:
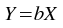
The best-fit is found by minimizing the weighted sum of squared residuals:
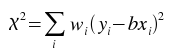
for b,
where wi is the weight at index i.
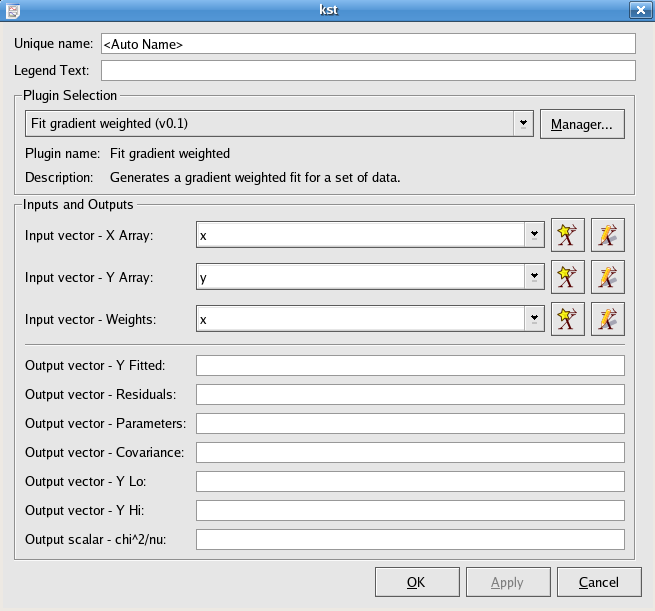
The array of x values for the data points to be fitted.
The array of y values for the data points to be fitted.
The array containing weights to be used for the fit.
The array of y values for the points representing the best-fit line.
The array of residuals, or differences between the y values of the best-fit line and the y values of the data points.
The parameter b of the best-fit.
The estimated covariance matrix, returned row after row, starting with row 0.
The corresponding value in Y Fitted minus the standard deviation of the best-fit function at the corresponding x value.
The corresponding value in Y Fitted plus the standard deviation of the best-fit function at the corresponding x value.
The value of the sum of squares of the residuals, divided by the degrees of freedom.
The Fit linear plugin is identical in function to the
Fit gradient weighted
plugin with the exception that the weight value wi
is equal to 1 for all index values i. As a result, the
Weights (vector) input does not exist.
The Fit linear weighted plugin performs a weighted least-squares fit to a straight line model:
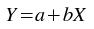
The best-fit is found by minimizing the weighted sum of squared residuals:
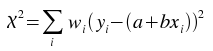
for a and b,
where wi is the weight at index i.
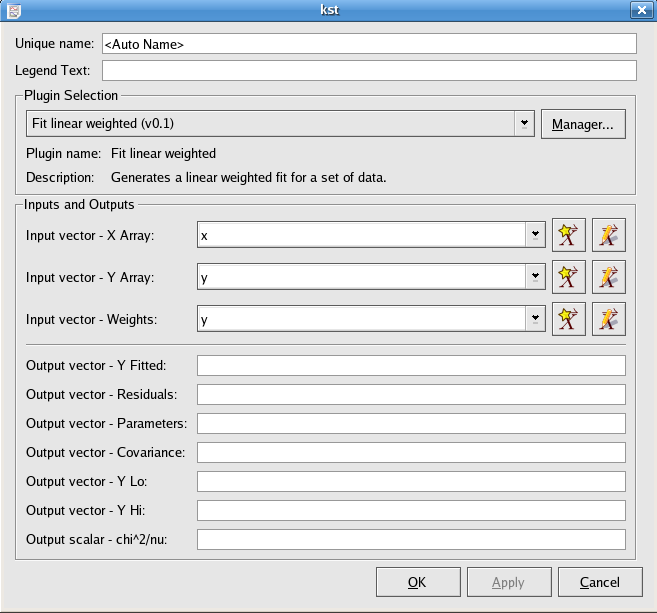
The array of x values for the data points to be fitted.
The array of y values for the data points to be fitted.
The array containing weights to be used for the fit.
The array of y values for the points representing the best-fit line.
The array of residuals, or differences between the y values of the best-fit line and the y values of the data points.
The parameters a and b of the best-fit.
The estimated covariance matrix, returned row after row, starting with row 0.
The corresponding value in Y Fitted minus the standard deviation of the best-fit function at the corresponding x value.
The corresponding value in Y Fitted plus the standard deviation of the best-fit function at the corresponding x value.
The value of the sum of squares of the residuals, divided by the degrees of freedom.
The Fit linear plugin is identical in function to the
Fit linear weighted
plugin with the exception that the weight value wi
is equal to 1 for all index values i. As a result, the
Weights (vector) input does not exist.
The Fit Lorentz weighted plugin performs a weighted non-linear least-squares fit to a Lorentzian model:

An initial estimate of
a=(maximum of the y values),
x0=(mean of the x values), and
=(the midpoint of the x values)
is used. The plugin subsequently iterates to the solution
until a precision of 1.0e-4 is reached or 500 iterations have been performed.
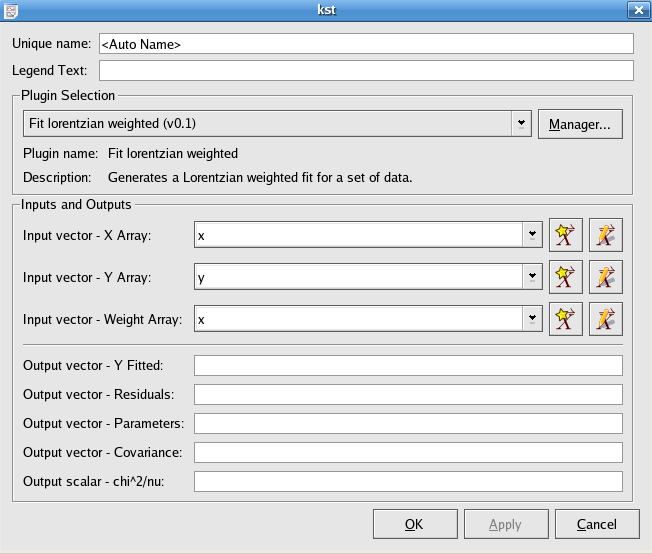
The array of x values for the data points to be fitted.
The array of y values for the data points to be fitted.
The array of weights to use for the fit.
The array of fitted y values.
The array of residuals.
The best fit parameters
x0,
 , and
, and
a.
The covariance matrix of the model parameters, returned row after row in the vector.
The weighted sum of squares of the residuals, divided by the degrees of freedom.
The Fit Lorentz plugin is identical in function to the
Fit Lorentz weighted
plugin with the exception that the weight value wi
is equal to 1 for all index values i. As a result, the
Weights (vector) input does not exist.
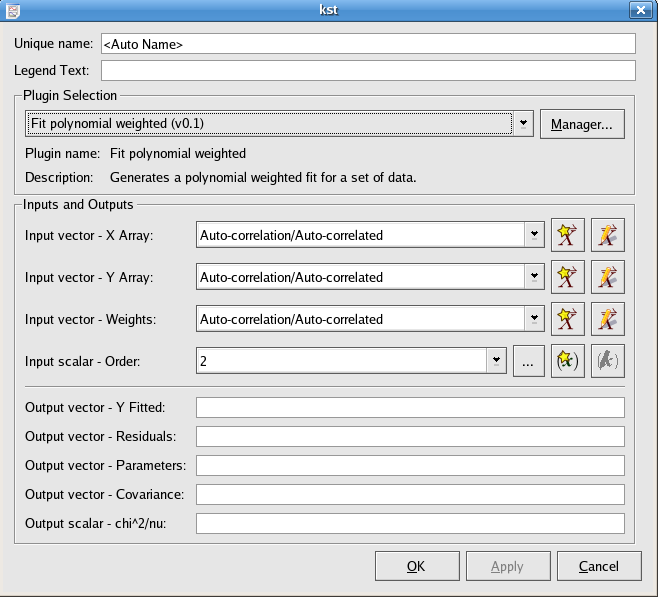
The Fit polynomial weighted plugin performs a weighted least-squares fit to a polynomial model:
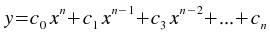
where n is the degree of the polynomial model.
The array of x values for the data points to be fitted.
The array of y values for the data points to be fitted.
The array of weights to use for the fit.
The order, or degree, of the polynomial model to use.
The array of fitted y values.
The array of residuals.
The best fit parameters c0,
c1,...,
cn.
The covariance matrix of the model parameters, returned row after row in the vector.
The weighted sum of squares of the residuals, divided by the degrees of freedom.
The Fit polynomial plugin is identical in function to the
Fit polynomial weighted
plugin with the exception that the weight value wi
is equal to 1 for all index values i. As a result, the
Weights (vector) input does not exist.
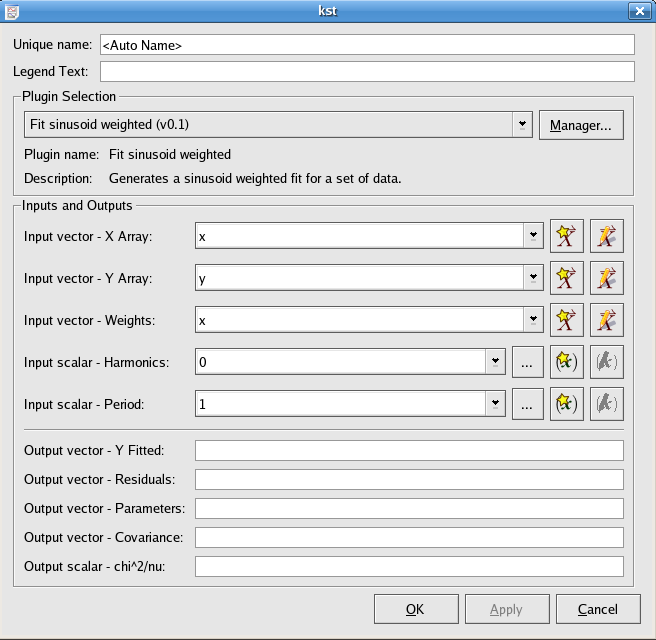
The Fit sinusoid weighted plugin performs a least-squares fit to a sinusoid model:
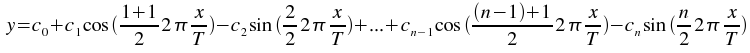
where T is the specified period,
and n=2+2H, where
H is the specified number of harmonics.
The array of x values for the data points to be fitted.
The array of y values for the data points to be fitted.
The array of weights to use for the fit.
The number of harmonics of the sinusoid to fit.
The period of the sinusoid to fit.
The array of fitted y values.
The array of residuals.
The best fit parameters c0,
c1,...,
cn.
The covariance matrix of the model parameters, returned row after row in the vector.
The weighted sum of squares of the residuals, divided by the degrees of freedom.
The Fit sinusoid plugin is identical in function to the
Fit sinusoid weighted
plugin with the exception that the weight value wi
is equal to 1 for all index values i. As a result, the
Weights (vector) input does not exist.
Would you like to make a comment or contribute an update to this page?
Send feedback to the KDE Docs Team